 |
Ein Spektrum besteht nicht nur aus deutlich getrennten Peaks, sondern öfters überlappen Peaks zu sogenannten Multipletts. Für die Dekomposition (oder Trennung) von Multipletts muß ein Fit verwendet werden und damit ist eine Beschreibung der Peakform notwendig. Anderenfalls ist es nicht möglich, die korrekte Anzahl von Peaks zu finden und eine gute Beschreibung des Spektrums zu erhalten.
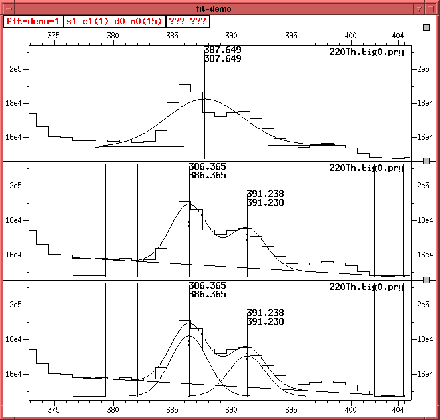
Als Beispiel, was passieren kann wenn man ein Multiplett falsch fittet, zeigt Abbildung 4.5 in der oberen Scheibe einen Quickfit. Wie man sieht, kann dieser die zwei Peaks nicht trennen. In der mittleren Scheibe wurde ein normaler Fit durchgeführt, bei dem zwei Peakmarker gesetzt waren und in der unteren Scheibe wird die Dekomposition angezeigt. Die Dekomposition kann mit den folgenden Kommandos angezeigt oder versteckt werden:
tv window show fit decomposition
tv window show fit decomposition
oder den Hotkeys md oder ud.
 |
TV verwendet eine modifizierte Gaußfunktion mit linkem und rechtem Tail und einer Stufe. Parameter der Gaußfunktion sind Position, Volumen und Breite, sowie linker und rechter Tail und Höhe und Breite der Stufe (siehe Abschnitt D.1 ). Für jeden gefitteten Peak gibt es diese sieben Parameter. Um die Anzahl der freien Parameter einzuschränken, kann man einzelne mit einem festen Wert belegen oder Korrelationen zwischen ihnen herstellen, z.B. alle Breiten gleichsetzen. Die Parameter für die Stufe und den Tail können meistens vernachlässigt werden, die für den Untergrund können gleichzeitig mit den Peaks gefittet werden, oder im Voraus in separaten Untergrund-Bereichen. Zur Wahl der Peak- und Untergrund-Funktion oder ob bestimmte Parameter angepaßt werden sollen oder nicht, werden die folgenden Kommandos verwendet (siehe Abschnitt 6.4.7 für die Kommandos des Menus fit function und Abschnitt 6.4.12 für Befehle des Menus fit parameter).
Um eine bestimmte Peak-Funktion zu aktivieren (standardgemäß ist continuous-exp-tail/arctan-step aktiv), verwendet man:
tv fit function peak activate {cont additive-tail/erf-step}
Man kann einen Parameter immer mit einem Wert belegen und diesen festhalten, d.h. TV verbieten ihn anzupassen, oder den Parameter frei setzen und ihn von TV fitten lassen.
Mit dem folgenden Befehl setzt man den Grad des Untergrundpolynoms (Standardwert ist 2) und hält diesen fest:
tv fit parameter background degree degree
tv fit parameter background hold
und aktiviert den Exponentialterm, indem man den Parameter FAC (siehe Abschnitt D.2) auf einen Wert ungleich 0 setzt:
tv fit parameter factor-background number number
tv fit parameter factor-background hold
Die Skalierung des Exponentialterms wird folgendermaßen gesetzt:
tv fit parameter exponent-background number number
tv fit parameter exponent-background hold
Alle Parameter, die mit Kommandos aus dem Menu fit parameter beeinflußt werden können, sind in Tabelle 4.7 zusammengestellt.
| Parameter | Bedeutung |
| background | Grad der Untergrund-Funktion. |
| exponent-background | Skalierung des Exponentialterms (siehe Abschnitt D.2. |
| factor-background | Faktor des Exponentialterms (siehe Abschnitt D.2). |
| position | Position. |
| sh | Höhe der Stufe. |
| sw | Breite der Stufe. |
| tl | Linker Tail. |
| tr | Rechter Tail. |
| volume | Volumen. |
| width | Breite. |
Es ist wichtig, die optimale Funktion zu wählen, um die Parameter zu optimieren. Die richtig Fit-Funktion gibt den Erwartungswert für den Inhalt jedes gefitteten Kanals. Da die gemessenen Werte einer Wahrscheinlichkeitsverteilung folgen, ist ihre Wahrscheinlichkeit, verglichen mit der erwarteten Funktion, für jeden Kanal bekannt. Für einen bestimmten Satz von Parametern kann eine Gesamtwahrscheinlichkeit, als Produkt der Wahrscheinlichkeiten der einzelnen Kanäle, ausgerechnet werden. Für den optimalen Satz von Parametern sollte sich die größte Wahrscheinlichkeit ergeben. Dieser Satz wird bestimmt, indem man das Maximum des Produktes, in Abhängigkeit von den Parametern, sucht (Maximum Likelihood).
Standardmäßig wird angenommen, daß die Kanalinhalte einer Gaußverteilung folgen. In diesem Fall erhält man die größte Wahrscheinlichkeit durch -Minimierung (siehe Abschnitt D.3). Unglücklicherweise ist das nicht anwendbar, wenn die Erwartungswerte für die Inhalte einzelner Kanäle in der Größenordnung von eins liegen. In dem Fall werden die Werte durch eine Poissonverteilung beschrieben. Die Fit-Funktion schätzt offensichtlich die Inhalte des Spektrums falsch ab. Die Fehlabschätzung hängt nicht vom Integral der gefitteten Daten ab, sondern von den Amplituden, d.h. die Größe des Fit-Bereichs spielt keine Rolle.
Neben der Minimierung des kann TV auch die Poissonverteilung maximieren (siehe Abschnitt D.3). Die Resultate, die man durch diese Methode erhält, sind so lange korrekt, wie die Spektren nur inkrementiert oder addiert wurden. Für normierte und subtrahierte Spektren ist die Varianz der Daten, die der Poissonverteilung folgen, nicht definiert und daher ist die Methode für diese Spektren nicht anwendbar. Auf Daten, die gemäß der Gaußverteilung verteilt sind, ist diese Methode hingegen anwendbar. Als Schluß aus dem gerade Gesagten kann man ziehen, daß keine der Verteilungsfunktionen korrekte Ergebnisse liefert, falls Spektren mit geringer Statistik subtrahiert wurden.
Zwischen den Meßfunktionen wird folgendermaßen umgeschaltet:
tv fit measure activate {dy- y- poisson}